There are an almost infinite number of blogs and sites dispensing advice, sharing looks, swapping recipes or just showing off aesthetically pleasing things. (The Guardian, 2011)
Infinity is very big, and “almost infinite” is just as big. To try and grasp a sense of the infinite is difficult, if not almost impossible.
Modernist architecture promoted the prospect of unconstrained space claiming to allow infinite possibilities for movement. The architecture did not tell you where to go and what to do. Wall planes seemed not to terminate at orthogonal junctions, but appeared as fragments of planes apparently stretching to infinity, as supposed in Mies Van der Rohe’s Barcelona Pavilion.
 Vanishing points in perspective drawings are infinitely far away, and cameras usually have an infinity setting that ensures that objects a long way off are in focus.
Vanishing points in perspective drawings are infinitely far away, and cameras usually have an infinity setting that ensures that objects a long way off are in focus.
Diagrams showing the sun’s rays hitting a surface on Earth are drawn parallel to each other, which is the condition of adjacent rays emanating from a point source at an infinite distance.
So infinity is ever present in geometry, apparatuses, architecture, maths, and language. But how big is it?
Infinity is clearly beyond imagining, which takes us into the realms of the Kantian sublime: “even to be able to think the given infinite without contradiction requires a faculty in the human mind that is itself supersensible.” (p.138)
I wonder if YouTube can help: that vast, but by no means infinite, array of arbitrary animated presentations and imaginings.
The closest I’ve come to a feeling of the infinite is from staring at a 5 minute fractal zoom. These are animated visualisations at ever increasing detail of the Mandelbrot set of self similar but varying twirls and twists of infinitely detailed filigree patterns. Visualisations of the Mandelbrot set are generated by a relatively short computer programme that involves an extremely large number of iterations (repeated calculations). The number series being represented revolves around the simple formula Z = Z*Z + C.
According to the author of one such animated deep zoom,
… if the first frame were the size of the visible universe, the last frame would be the size of a single bacterium, and the final baby Mandelbrot Set shown would be approximately 0.02 mm in diameter, which is microscopic to the naked eye! Even more remarkable, this barely even scratches the surface of the infinite depths of the Mandelbrot Set!
http://www.youtube.com/watch?v=VSDI84Mm-hI (You might want to turn off the sound.)
Over a period of five minutes you will zoom in from something the size of the known universe to the size of a bacterium, by doubling the scale every three seconds. Another few minutes and you would be at the scale of the Higgs Boson particle, and beyond.
This scale transitioning is comparable to the number series created by placing a grain of rice on a chessboard square, doubling it on the next square, doubling that for the next square and so on. The last square to be filled would have to be big enough to take 2 to the power of 63 grains of rice (plus 1), by some calculations requiring a grainstore with a footprint of about 25 kilometers square. The point of the demonstration is that we have little idea at the start of the doubling exercise that it will result in something so far off the scale … a rapid movement towards infinity … almost.
The speed at which we can navigate these scale transitions has to draw on our “supersensible” mental faculties, and is attributable to the properties of exponential number series, about which we seem to have very poor intuitions.
The boundary to the Mandelbrot set is characterised by massive variation and is infinite in extent. Zooming into this tangled field must be what it’s like to travel through an abyss. However deep we probe the stronger the impression that there’s after all nothing there: infinite extent bereft of meaning, unlike the lived universe, and hopefully unlike the Internet … almost.
Bibliography
- Carter, Kate (2011). “Bloggers! Life & style needs you” The Guardian, 28 July 2011.
http://www.guardian.co.uk/lifeandstyle/2011/jul/28/bloggers-life-style
- Kant, Immanuel, and Paul Guyer. 2000. Critique of the Power of Judgment. Cambridge: Cambridge University Press.
- Rasmussen, Eric (2006). Nearly Infinite, Eric Rasmussen’s Webloghttp://www.rasmusen.org/x/2006/05/02/1158/
- Also see post on the sublime and vibration, and the sky.
Coda
Jacques Derrida refers in many places to the infinite. “Mise en abyme” means ‘putting into infinity’, or standing at an abyss or chasm, the effect you get when standing between two parallel facing mirrors and look into the infinitely receding reflections. Mise en abyme is also evident where a picture appears within a picture, or the dreamer encounters a dream within a dream. Derrida also uses the term to account for the interreferentiality of texts (intertextuality), and the elusive production of meaning. “… it can be called the play of the trace. The play of a trace which no longer belongs to the horizon of Being, but whose play transports and encloses the meaning of Being: the play of the trace, or the différance, which has no meaning and is not. Which does not belong.
There is no maintaining, and no depth to, this bottomless chessboard on which Being is put into play (Derrida, 1982 p.22).
- Derrida, Jacques. 1982. Différance. Margins of Philosophy: 3-27. Chicago: University of Chicago press.
- Coyne, Richard. 2011. Derrida for Architects. London: Routledge.
I also feel the need to add (13 Dec 2011)
William Blake – Auguries of Innocence
To see a world in a grain of sand,
And a heaven in a wild flower,
Hold infinity in the palm of your hand,
And eternity in an hour. …

There is a similar instance of Mandelbrot sets zoom in film editing – the Seamless Editing technology. At the beginning of Limitless (2011), the camera zoomed across blocks and taxis, it seems like the camera will never stop, and the movie will be endless.
Looking for infinity is more like questing for perfect, it is something that human will never possible to achieve, but maybe what we want is just close to it.
Universe is one of the infinity examples. We all knew the immense of our cosmic, but it is not until I watch the video, Star Size Comparison on YouTube, I realized we are so minor in the Universe, if Earth is a dust compared with the size of the biggest star we have found so far, it is less than a bacterium compared with the whole universe. http://www.youtube.com/watch?v=HEheh1BH34Q
Even though there are thousands millions of web sites on the Internet, but I still fail to found answers at times when I have questions.
Norman McLaren created the special effect “infinite zoom” in his animation without using any computer technology. this technique was used again in the “2001; space Odyssey”.
it is sad that when we know exactly that the internet is such a huge database, but not knowing where and how to find our answers. I think that either Baudrillard or McLuthan mentioned that the internet is like the highway, leading to different places, even though your destination is just one.
I remember when we were small, there is a fable that the king asked one prince who want to marry his daughter: how many hairs do I have? the prince answered: just as many as the stars in the sky.(p.s: this answer is not applicable nowadays.)
the prince avoid the problem by exchange or replace the ‘infinite’ for another infinite. however, if we want, the number of hair is countable. for the number of stars, it is indeed uncountable. the universe space is infinite, the time is infinite.
but I do wonder if the internet could be infinite. if we don’t update the storage of internet, we may run out of the internet virtual space afterall. while, from the aspect of information, since we cannot count information by character or words, but by the contents, it is uncountable itself. therefore, the internet for me, is both infinite and limited.
There seem to be other videos that attempt the same. The most famous representation of scale sequence is “Powers of Ten,” made in 1977: http://www.youtube.com/watch?v=0fKBhvDjuy0. By way of contrast I feel it’s the suggestion of infinite detail that makes fractal images evocative, and disturbing.
How big is the ?
?
As Immanuel Kant referred to defining infinity is beyond the human mind, so did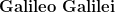 (1564 – 1642), who is said to be one of the fist modern thinkers to seriously confront the enigma of infinite. In fact he considered the set of natural numbers
(1564 – 1642), who is said to be one of the fist modern thinkers to seriously confront the enigma of infinite. In fact he considered the set of natural numbers 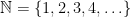 and the set of perfect squares
and the set of perfect squares 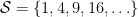 . Since all the numbers in
. Since all the numbers in  are in
are in  , we might expect that
, we might expect that 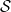 is smaller than
is smaller than  , or ‘a part is smaller than the whole’:
, or ‘a part is smaller than the whole’:
However, counter intuitively enough, since each perfect square in
Also, I have read that (1845 – 1918) is one of the greatest mathematicians in the history, and he is the father of infinity. Cantor’s diagonal method proves the existence of an infinity of infinity of infinity… of infinity…!
(1845 – 1918) is one of the greatest mathematicians in the history, and he is the father of infinity. Cantor’s diagonal method proves the existence of an infinity of infinity of infinity… of infinity…! impossible .
impossible .![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) , that is, all the points or real numbers from
, that is, all the points or real numbers from  to
to 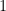 . Regarding
. Regarding  and
and 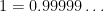 etc., we can express all the numbers in
etc., we can express all the numbers in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) using decimal expansions. So we can name all the points as
using decimal expansions. So we can name all the points as 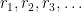 and list them in the following way.
and list them in the following way.
Although this did not make sense at all when I first encountered this, I found his proof very very fascinating and fairly understandable even for non-mathematically minded people including myself, if not
Cantor proved that there is always an uncountable sets of natural numbers, beyond an infinitely many sets of natural numbers. Suppose we have a line segment
Again, we can see that there are infinitely many decimal numbers in
For each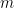 and
and 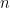 let
let 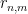 be the
be the 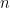 -th decimal element of the
-th decimal element of the 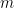 -th sequence on the list. So, for instance,
-th sequence on the list. So, for instance, 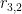 is the third element of the second sequence. So in the above list
is the third element of the second sequence. So in the above list  . We now define a
. We now define a  number
number 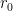 in
in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) as follows:
as follows: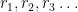 as above, we look at the diagonal elements
as above, we look at the diagonal elements  in the list. Thus, in the listing above, we consider:
in the list. Thus, in the listing above, we consider:
Given a listing of
Then we apply the following rule:
So, for our example,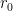 would be
would be  . This is certainly the decimal number that should be listed, since
. This is certainly the decimal number that should be listed, since 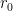 is clearly in
is clearly in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) . However, each decimal element of
. However, each decimal element of 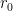 is at least, by our construction, different from
is at least, by our construction, different from 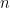 -th decimal number of any real number on our list. Hence, no matter how we list the real numbers in
-th decimal number of any real number on our list. Hence, no matter how we list the real numbers in ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=FFFFFF&fg=000&s=0&c=20201002) with decimal representation, we can construct
with decimal representation, we can construct 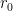 in such a way that it is definitely not on any possible listing.
in such a way that it is definitely not on any possible listing.
This shows that there are more real numbers than natural numbers! Since we know that there are (countably ) infinitely many natural numbers, there is an infinity that is greater than the infinity!!
Now that if we consider the infinite sequence of human interactions, applying Cantor’s argument, we can prove that there are uncountably, infinitely many human interactions. In particular, we must note that this is not due to internet, or technology, but due to the fact that almost all of us communicate and interact with each other. Thus, the internet or technologies are not something that can increase possibilities of human interactions to a great extent, but rather they change the nature of interactions. At the end of the day, especially as a DDM student, I should always remember and consider that I am a medium who do change people’s interactions by committing myself to the society.
Finally, I hope this entry is not ‘just showing off aesthetically pleasing things’.
P.S. I found that infinity is really infinite (if this makes sense at all) and Cantor might have possessed a faculty in his mind that was supersensible! Also, I enjoyed using in WordPress!
in WordPress!
Forgot to define what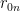 is. Above, I denoted by
is. Above, I denoted by 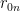 the
the 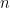 -th decimal number of our new number
-th decimal number of our new number 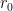 .
.
I couldn’t even work out how to represent the formula z equals z squared plus c. Latex certainly facilitates representations of infinitIty, or at least the mathematical sublime. But I’m being oblique. Terrific comment. Thanks ddmAyumi. I’ll ponder Cantor’s proof. That something infinitely big can be smaller than something else is taxing. In fact we could try some EEG neural imaging of what happens when people contemplate infinity. I’ll ask Panos Mavros.